Light and Materials
Two values are used to describe the optical properties which determine how light interacts with a material. They are generally represented as a complex number. The complex refractive index (ñ) consists of the index (n) and extinction coefficient (k):
![]()
Alternatively, the optical properties can be represented as the complex dielectric function:
![]()
with the following relation between conventions:
![]()
The index describes the phase velocity of light as it travels in a material compared to the speed of light in vacuum, c:
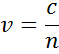
Light slows as it enters a material with higher index. Because the frequency of light waves remains constant, the wavelength will shorten. The extinction coefficient describes the loss of wave energy to the material. It is related to the absorption coefficient, , as:
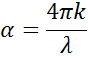
Light loses intensity in an absorbing material according to Beer’s Law:
![]()
Thus, the extinction coefficient relates how quickly light vanishes in a material. These concepts are demonstrated in Figure 2 where a light wave travels through two different materials of varying properties before returning to the ambient.
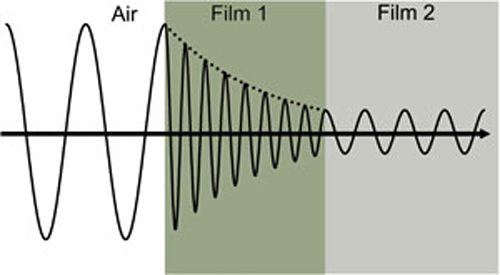
Wave travels from air into absorbing Film 1 and then transparent Film 2. The phase velocity and wavelength change in each material depending on index of refraction (Film 1: n=4, Film 2: n=2).
The optical constants for TiO2 from the ultraviolet (UV) to the infrared (IR), as shown in Figure 3. The optical constants are determined by wavelength with absorption (k>0) occurring in both UV and IR due to different mechanisms that take energy from the light wave. IR absorption is commonly caused by molecular vibration, phonon vibration, or free-carriers. UV absorption is generally due to electronic transitions, where light provides energy to excite an electron to an elevated state. A closer look at the optical constants in Figure 3 shows that real and imaginary optical constants are not independent. Their shapes are mathematically coupled through Kramers-Kronig consistency.
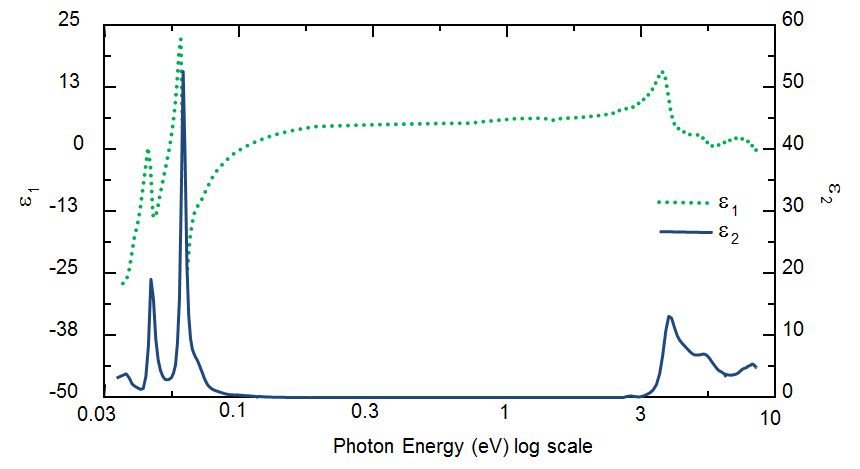
Complex dielectric function for TiO2 film covering wavelengths from the infrared (small eV) to the ultraviolet (high eV).

